Doc Réduction d'endomorphismes
Réduction rationnelle des endomorphismes
Ce document traite de la réduction des endomorphismes sur un corps commutatif tel qu'il a été enseigné à des étudiants de L3 en liaison avec des exercices interactifs.
On fixe un corps commutatif et un espace vectoriel de dimension finie . On note l'ensemble des endomorphismes de . Il est muni d'une structure d'algèbre ( -espace vectoriel + anneau + compatibilité entre les lois).
V Facteurs invariants et décomposition rationnelle (Frobenius)
VI Diagonalisation et trigonalisation
VIII Tous les exercices WIMS utilisés
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
I Polynômes d'endomorphismes
Lemme
Proposition
Démonstration
- ;
- .
Les , , ..., sont éléments de l'espace vectoriel qui est de dimension . Donc, il existe des éléments , ... , de non tous nuls tels que . Le polynôme est un polynôme non nul appartenant au noyau de .
Tout idéal de est principal, c'est-à-dire de la forme pour un polynôme .
Définition
Définition
Exemple
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
II Sous-espaces stables
Définition
Proposition
Démonstration
Exemple
- Si
est un polynôme,
et
sont des sous-espaces
stables pour
.
- Si
est une droite stable, il existe
tel que
pour tout
. On a alors
.
En prenant pour
le polynôme minimal
, on obtient
que
et donc que
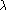 est une racine du polynôme
minimal de
.
est une racine du polynôme
minimal de
.
Théorème [Théorème des noyaux]
Note
- tout vecteur de s'écrit de manière unique sous la forme avec ;
- pour tout , et tout vecteur de s'écrit sous la forme (autrement dit ) ;
- si est une famille d'applications linéaires de dans un espace vectoriel , il existe une unique application linéaire de dans coïncidant avec sur .
En particulier, les projecteurs commutent avec .
Démonstration
Exercice
Exercice
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
III Sous-espaces cycliques
On note le polynôme unitaire engendrant l'idéal noyau de l'homomorphisme de dans . C'est un diviseur de .
Proposition
Définition
Proposition
Démonstration
On développe le déterminant de par rapport à la première colonne, puis le deuxième déterminant obtenu par rapport à la dernière colonne. On obtient
Les deux lemmes suivants serviront à la démonstration de la proposition qui les suit.
Lemme
Démonstration
Lemme
Démonstration
On montre par récurrence que si , ... sont des vecteurs et que les polynômes sont premiers deux à deux, alors
Proposition
- Il existe un vecteur tel que . Plus précisément, si est une base donnée, peut être choisi dans cette base.
La proposition précédente est l'analogue des assertions suivantes dans un groupe abélien fini : l'exposant de est égal au ppcm des ordres des éléments de et il existe un élément de dont l'ordre égal à l'exposant de de .
Démonstration
-
Le polynôme
divise
pour tout vecteur
, donc
divise
. Réciproquement, prenons une base
de
.
Soit
le ppcm des
. Si
,
,
on a Donc divise .
- Ecrivons la décomposition en éléments irréductibles de
:
avec les premiers entre eux deux à deux. On a avec . Le polynôme minimal de la restriction de à est un diviseur de . Le polynôme minimal de est alors le produit des , mais il vaut aussi , ce qui prouve qu'en fait . Sur chacun des sous-espaces (stables par ), prenons une base . Le ppcm des pour est égal à . Il existe donc un élément de telle que . Le vecteur vérifie alors , ce qui démontre la proposition.
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
IV Dualité
IV-1 Survol des propriétés de la dualité
IV-2 Dualité et sous-espace stable
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
IV-1 Survol des propriétés de la dualité
Définition
Proposition
Proposition
Définition
Proposition
Proposition
Démonstration
Une notation agréable pour noter la dualité est d'écrire
IV-2 Dualité et sous-espace stable
Définition
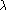 nulles sur
.
nulles sur
.
Proposition
Démonstration
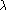 une forme linéaire appartenant à
. Pour
,
une forme linéaire appartenant à
. Pour
,
Proposition
Démonstration
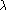 appartient à
.
appartient à
.
Proposition
Démonstration
- injective car ;
- surjective car tout vecteur est la somme d'un vecteur de et d'un vecteur de ;
IV-3 Exercices
Exercice
Exercice
Soient et deux espaces de dimension finie et une application linéaire de dans .
- Montrer que
et que
Solution
Rappelons que est l'application linéaire de dans défini par avec et ou en utilisant la forme bilinéaire définie par ,On a alors les équivalencesDonc si et si , on a , donc
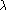 appartient à l'orthogonal
de
. On obtient donc l'inclusion
.
appartient à l'orthogonal
de
. On obtient donc l'inclusion
.
Réciproquement, on peut invoquer les dimensions. On peut aussi le faire ``explicitement'' : soit , on choisit un supplémentaire de dans . On définit si et si . Cette définition ne dépend pas du choix de grâce à la propriété que si ) et définit une application linéaire. On a bien .
...
- Montrer que
est surjective si et seulement si
est injective et que
est injective si et seulement si
est surjective
Solution
Cela se déduit de la question précédente :
est surjective est injective.
Exercice
Soit une application linéaire de dans . Soit un sous-espace de , son orthogonal dans . On note .
- Montrer que
est l'orthogonal de
dans
.
Solution.
- Si
et
sont deux sous-espaces supplémentaires de
, montrer que
et
sont supplémentaires dans
.
SolutionSoit . Alors, pour tout , pour tout , et . Donc, comme et sont supplémentaires, pour tout . Donc .
On peut ensuite invoquer les dimensions. Ou : soit . On définit comme l'unique forme linéaire coincidant aec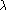 sur
et valant 0 sur
et
comme l'unique forme linéaire
coincidant avec
sur
et valant 0 sur
et
comme l'unique forme linéaire
coincidant avec
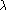 sur
et valant 0 sur
.
On a bien
. De plus,
, puisqu'elle est nulle sur
et de même
.
sur
et valant 0 sur
.
On a bien
. De plus,
, puisqu'elle est nulle sur
et de même
.
V Facteurs invariants et décomposition rationnelle (Frobenius)
V-1 Le théorème des facteurs invariants
V-3 Cas des dimensions 2, 3 et 4
V-5 S'exercer : Invariants, classes de similitude.
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
V-1 Le théorème des facteurs invariants
Théorème [Frobenius]
- .
Donnons déjà quelques conséquences :
- Le polynôme minimal de est donné par : .
- Le polynôme caractéristique est le produit des : .
- Le polynôme est un multiple de ; c'est le théorème de Cayley-Hamilton : .
- Les polynômes
et
ont mêmes facteurs irréductibles, ce qui se traduit par
Démonstration [ Existence ]
- On choisit un vecteur tel que .
- On cherche un supplémentaire de stable par .
- On applique l'hypothèse de récurrence à .
Cherchons un sous-espace cyclique dans le dual de . Pour cela, prenons une forme linéaire
 qui ne s'annule pas sur
et telle que
soit égal à
: par exemple,
prenons
qui ne s'annule pas sur
et telle que
soit égal à
: par exemple,
prenons
 telle que
,
,
,
avec
. Cela est possible car les vecteurs
forment un système libre.
{footnote}
Trouver
telle que
,
,
,
avec
. Cela est possible car les vecteurs
forment un système libre.
{footnote}
Trouver
 revient à résoudre un système linéaire.
{footnote}
Calculons
.
revient à résoudre un système linéaire.
{footnote}
Calculons
.
Si , on a et . Remarquons que si avec et , on a
On a ainsi trouvé un sous-espace cyclique pour , qui est stable par de polynôme minimal .
Montrons que est d'intersection nulle avec l'orthogonal de .
Soit un élément de . Il est de la forme avec ou . Supposons non nul. Pour tout polynôme ,
Une fois démontré que , la comparaison des dimensions implique que . Et le sous-espace est stable par .
Montrons maintenant l'unicité des éléments . Commençons par un lemme simple mais important.
Lemme
Supposons que est somme directe de où et sont des sous-espaces stables par . Alors, .
Démonstration
Démonstration [ Unicité ]
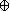 |
 |
 | ||||
 |
 |
 |
 |
 | ||||||
 |
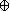 |
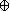 |
Remarque
V-2 Quelques conséquences
Proposition
Démonstration
- Les restrictions de
à
et de
à
ont même matrice dans les bases respectives
et
.
- s'identifie au dual de grâce à l'application linéaire qui est une bijection (injection + même dimension). On a donc , et . On raisonne alors par induction.
Définition
Théorème
Démonstration
Proposition [Réduction de Frobenius d'une matrice]
Proposition
Démonstration
 . La dimension de
est égale au degré de
.
Donc
et
.
. La dimension de
est égale au degré de
.
Donc
et
.
Proposition [Cas particulier des endomorphismes nilpotents]
La matrice sera aussi notée , car c'est un cas particulier d'un bloc de Jordan.
Le diagramme de Young représenté est associé à un espace vectoriel de dimension 13 somme directe de 5 sous-espaces -cycliques. Ses invariants de similitude sont .
V-3 Cas des dimensions 2, 3 et 4
-
- : nécessairement , la suite des invariants est .
- : nécessairement , la suite des invariants est .
-
- : nécessairement , la s.ite des invariants est .
-
: nécessairement,
avec
et
de degré 1
(il n'est pas possible que
 soit irréductible, car
soit irréductible, car
 serait de degré
2 ou supérieur à 4 ...); on a
, la suite des invariants est
.
serait de degré
2 ou supérieur à 4 ...); on a
, la suite des invariants est
.
- : nécessairement, , la suite des invariants est .
Exercice
Solution
- : nécessairement , la suite des invariants est .
-
et
 est irréductible : nécessairement
,
la suite des invariants est
.
est irréductible : nécessairement
,
la suite des invariants est
.
-
et
avec
n'est pas irréductible :
- soit et la suite des invariants est ;
- soit et la suite des invariants est .
-
et
:nécessairement
. Deux
possibilités pour la suite des invariants :
- soit la suite des invariants est ;
- soit la suite des invariants est .
-
et
 est irréductible : ce n'est pas possible.
est irréductible : ce n'est pas possible.
- et avec : nécessairement , la suite des invariants est .
- et avec : nécessairement , la suite des invariants est .
- : nécessairement , la suite des invariants est .
V-4 Des exercices corrigés
Exercice
Soient , , trois polynômes irréductibles distincts sur un corps .
- Combien y a-t-il de classes de similitude
de matrices à coefficients dans
ayant comme polynôme minimal
et comme
polynôme caractéristique
? Pour chacune d'elles, donner
les invariants de similitude.
SolutionLes classes de similitude sont en bijection avec les suites de polynômes avec , et . Elles sont nécessairement de la formeavec et . D'où deux solutions :
- On prend
et
,
et
. Parmi les classes de similitudes
précédentes, quelles sont celles pour lesquelles la dimension de l'espace propre associé
à la valeur propre 1 est supérieure ou égale à 3 ?
Donner la matrice de Frobenius associée à une telle décomposition de Frobenius
il ne doit donc apparaître que des matrices compagnons.
SolutionLa condition impose que l'on est dans le premier cas. En effet, l'espace propre de pour la valeur propre 1 restreint à chacun des sous-espaces cycliques est de dimension 1 si divise le polynôme minimal de ce sous-espace cyclique et de dimension 0 sinon.
, . La matrice dans une base adaptée est alors
Exercice
Soit un espace vectoriel de dimension finie et un endomorphisme de . On suppose que où les sous-espaces vectoriels sont des sous-espaces stables par , cycliques pour de polynôme minimal respectif , , , . Quelle est la dimension de ? Donner les invariants de similitude de et écrire une décomposition de Frobenius de .
Solution
Exercice
Soit un espace vectoriel de dimension finie et un endomorphisme de . On suppose que le polynôme caractéristique de est et que le noyau de est un plan. Quelles sont les formes possibles de la réduite de Jordan ?
Solution
Exercice
Soit un espace vectoriel de dimension finie et un endomorphisme de . On suppose que le polynôme caractéristique de est et que le noyau de est un plan. Quelles sont les formes possibles de la réduite de Jordan ?à la valeur propre 1 est 2 car le sous-espace propre est de dimension 2. Les formes possibles de Jordan sont donc (à permutation près des blocs sur la diagonale)
V-5 S'exercer : Invariants, classes de similitude.
Nombre de classes de similitude I
Nombre de classes de similitude II
Nombre de classes de similitude III
VI Diagonalisation et trigonalisation
Définition
VI-1 Endomorphismes diagonalisables
VI-3 Endomorphismes trigonalisables
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
VI-1 Endomorphismes diagonalisables
Définition
Proposition
Démonstration
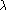 est la valeur
propre associée à
. Donc
qui est un diviseur de
est bien scindé et avec des racines simples (en fait,
).
est la valeur
propre associée à
. Donc
qui est un diviseur de
est bien scindé et avec des racines simples (en fait,
).
Réciproquement, supposons que avec pour . Les polynômes sont alors premiers deux à deux et on peut appliquer le théorème du noyau :
Supposons diagonalisable. Cherchons la décomposition de Frobenius de . On a . Rappelons que et que le produit des doit être égal à ( est donc la multiplicité de dans ). La seule possibilité combinatoire est que
Remarque
On remarque que étant donné un polynôme sans facteur multiple (les étant irréductibles) et un polynôme avec , il existe une unique classe d'endomorphismes semi-simples de polynôme minimal et de polynôme caractéristique . L'unicité est bien sûr fausse si on enlève la condition semi-simple comme on l'a vu dans un cas de dimension 4.
VI-2 S'exercer
Exercice
Trouver un vecteur propre
Matrice diagonalisable ?
Trouver un vecteur propre
Matrice diagonalisable ? Peut-on conclure
Petit QCM sur la diagonalisation
VI-3 Endomorphismes trigonalisables
Définition
Définition équivalente : Un endomorphisme est dit trigonalisable s'il existe une suite de sous-espaces vectoriels stables par telle que avec .
Proposition
Démonstration
Supposons maintenant que est scindé (et donc ). Le polynôme minimal de l'endomorphisme dual est lui aussi scindé. Donc, a un vecteur propre (non nul)
 dans
de valeur propre
dans
de valeur propre
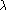 .
Soit
le noyau de la forme linéaire
.
Soit
le noyau de la forme linéaire
 . C'est un sous-espace vectoriel de
de
dimension
(hyperplan) stable par
car
est un sous-espace
de
stable par
: refaisons la démonstration : si
,
. C'est un sous-espace vectoriel de
de
dimension
(hyperplan) stable par
car
est un sous-espace
de
stable par
: refaisons la démonstration : si
,
VI-4 Exercices
Exercice
Dans les deux premières questions, est un endomorphisme diagonalisable de et l'ensemble de ses valeurs propres. Pour tout , on note l'espace propre associé.
-
Montrer qu'un sous-espace
de
est stable par
si et seulement si
est somme (alors
directe) des
pour
.
SolutionLe sous-espace propre est le noyau de avec le polynôme . Si est stable par , il en est de même de . En particulier, les sous-espaces sont en somme directe. D'autre part, la restriction de à est diagonalisable (son polynôme minimal n'a que des zéros simples). Si est l'espace propre de associé à la valeur propre , on a . Donc .
La réciproque est facile : il suffit de montrer que est stable par . Or si ,
-
En déduire que tout sous-espace de
stable par
possède un supplémentaire stable par
.
SolutionSoit un sous-espace stable par . Soit un supplémentaire de dans . Il est nécessairement stable par , car la restriction de à est une homothétie. Alors est un supplémentaire de dans stable par (on a , les dimensions sont OK et .
-
Soit un endomorphisme de dont le polynôme caractéristique est scindé. Supposons que tout sous-espace de stable par ait un supplémentaire stable. Montrer que est alors diagonalisable.
SolutionSupposons que n'est pas diagonalisable. Il existe alors une valeur propre et un vecteur tel que et . Soit le sous-espace engendré par . Il est stable par car . Donc il admet un supplémentaire stable par . On décompose avec et . En appliquant , ce qui vaut d'autre part . Donc, . Comme appartient à , on en déduit que appartient à ce qui est impossible.
- Contre-exemple si
n'est pas diagonalisable.
SolutionPrenons de matrice dans une base. Le sous-espace est stable par mais ne possède pas de supplémentaire stable par . Sinon, serait diagonalisable.
VII Décomposition de Jordan
VII-2 Formes de Jordan possibles
VII-3 Dimension de la somme des espaces propres
VII-4 Exercice : décomposition de Dunford explicitement
VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
VII-6 Vecteurs propres, blocs de Jordan pour les endomorphismes nilpotents
VII-8 Exercice : décomposition de Jordan-Chevalley
VII-9 Endomorphisme cyclique et commutant
VII-10 Carré d'un endomorphisme
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés
VII-1 Réduction de Jordan
Définition
Théorème
Démonstration
- décomposition primaire : ;
- décomposition de Frobenius sur chacun des
et de l'endomorphisme
en somme directe de sous-espaces cycliques :
avec un sous-espace cyclique de polynôme minimal , suite décroissante d'entiers avec . La matrice de restreinte à dans la base est un bloc de Jordan de taille .
Théorème
Démonstration
Montrons que commute avec . En effet, soit les projections de sur . Les sous-espaces étant obtenus par le théorème des noyaux, est un polynôme en et . On en déduit que commute avec et commute aussi avec et avec .
Montrons maintenant l'unicité. Ecrivons avec et des polynômes en . On en déduit que et commutent à et . Donc, est encore diagonalisable grâce au lemme qui suit et étant à la fois diagonalisable et nilpotent est nul. Donc, , .
Lemme
Démonstration
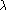 une valeur propre de
et
.
Montrons que
est stable par
. En effet, si
,
une valeur propre de
et
.
Montrons que
est stable par
. En effet, si
,
Exercice [ Et si les deux endomorphismes sont triangonalisables ]
Soient et des endomorphismes trigonalisables de qui commutent. Montrer qu'il existe une base de dans laquelle les matrices de et sont triangulaires. {sol} De manière générale, si est un polynôme, laisse stable . En effet, si , on a . Donc . Le polynôme caractéristique est scindé : avec les polynômes premiers entre eux deux à deux et en fait de la forme . On a (théorème des noyaux). De plus, trouver une base dans laquelle la matrice de est trigonalisable revient à trouver pour tout , des bases compatibles des sous-espaces pour variant. L'endomorphisme laisse stable chacun de ces sous-espaces et est trigonalisable sur chacun de ces sous-espaces.
{sol}
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-2 Formes de Jordan possibles
Exercice
Solution
| Réduction de Jordan | Nombre de blocs | Invariants | Diagramme de Young | Dim de l'espace propre |
|---|---|---|---|---|
| 2 |
| 2 | ||
| 1 |
| 1 |
La dimension de est 3 (polynôme caractéristique de degré 3).
| Réduction de Jordan | Nombre de blocs | Invariants | Diagramme de Young | Dim de l'espace propre |
|---|---|---|---|---|
| 3 |
| 3 | ||
| 2 |
| 2 | ||
| 1 |
| 1 |
On suppose de plus que l'espace propre associé à est un hyperplan et que l'espace propre associé à est un plan. Quelle est la réduction de Jordan ?
Solution
Exercice
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-3 Dimension de la somme des espaces propres
Proposition
Exercice
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-4 Exercice : décomposition de Dunford explicitement
Exercice
Trouver la décomposition de Dunford de la matrice/endomorphisme .
Solution
Alors, avec . On peut aussi écrire cela comme une solution du lemme chinois :
On a
Remarquons que si , la matrice est digonalisable et on a bien dans ce cas.
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
Soit un espace vectoriel de dimension finie et un endomorphisme.
- Soit
un sous-espace cyclique de
pour
de dimension
: il admet donc une base de la forme
Soit une forme linéaire ne s'annulant pas sur et s'annulant sur pour . Montrer que si est le sous-espace du dual de engendré par , l'orthogonal de est un supplémentaire de dans stable par .
SolutionMontrons que et sont en somme directe. Soit un vecteur de tel que pour tout . Alors pour tout . En prenant , on obtient , puis avec , , ... (système triangulaire).
Montrons maintenant que est de dimension . Dans le cas contraire, les formes linéaires seraient liées. Il existerait une combinaison linéaire nulle non triviale non nulle avec et . Donc sur le vecteur ,On a donc montré que . Le sous-espace est stable par . Donc son orthogonal est stable par .
- Application : on considère l'endomorphisme
dont la matrice dans une base
est
On indique que le polynôme caractéristique de est .- Calculer la dimension des noyaux des puissances successives de
.
SolutionOn calcule les puissances successives de :
Le noyau de est de dimension 2 (on peut vérifier que le noyau de est engendré par les vecteurs et ), le rang de est 1. On en déduit que , , .
- En déduire la forme de Jordan de
(sans calculer de changement de base).
SolutionLe nombre de blocs de Jordan de taille supérieure ou égale à 1 est donc 2, le nombre de blocs de Jordan de taille supérieure ou égale à 2 est donc 4-2=2, le nombre de blocs de Jordan de taille supérieure ou égale à 3 est donc 5-4=1, le nombre de blocs de Jordan de taille supérieure ou égale à 4 est donc 0. Il y a donc un bloc de taille 2 et un bloc de taille 3 :
- En utilisant la méthode indiquée dans la première question, calculer une base dans laquelle
la matrice de
est la matrice de Jordan trouvée à la question précédente.
SolutionOn choisit un vecteur tel que , par exemple dans les vecteurs de la base canonique. Prenons, . . On a alors . Soit . On cherche une forme linéaire telle que et telle que , . Par exemple : en représentant par une matrice ligne : .
On calcule une base du sous-espace cyclique engendré par dans . On aL'orthogonal de est un supplémentaire de stable par . Il est donné par les équations
Une base de est donnée par et . On doit maintenant choisir un vecteur dans tel que . On prend . Soit . Dans la base , la matrice de est la matrice de Jordan écrite plus haut : sion a .
- Calculer la dimension des noyaux des puissances successives de
.
Exercice
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-6 Vecteurs propres, blocs de Jordan pour les endomorphismes nilpotents
On suppose désormais que est nilpotent. On s'y ramène en utilisant le théorème des noyaux puis en étudiant plutôt que . Soit son polynôme minimal.
Proposition
Démonstration
On en déduit le cas général.
Théorème
Démonstration
On peut lire cette formule sur le diagramme de Young de . Le terme est égal au nombre de lignes sur la -ième colonne.
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-7 Quelques exercices
Exercice
Solution
Ses invariants sont .
Exercice
Solution
On a , donc la dimension du noyau est 4. On en déduit que la suite des invariants est de longueur 4. La seule possibilité est donc qu'il y ait 4 blocs de taille 2. Son diagramme de Young est
Exercice
Solution
La dimension du noyau de est égale à 3. On en déduit qu'il y a au plus 2 blocs (la dimension de ). Les diagrammes de Young possibles sont
Il y a trois classes de similitudes dont les invariants sont , , .
Exercice
Solution
Exercice
Soit la matrice .
-
Montrer que
est nilpotente et calculer la dimension des noyaux des
puissances successives de
. Donner la forme de Jordan
de la matrice
.
SolutionOn a et . On voit des relations sur les colonnes de : , . Donc l'image de est engendrée par , , et . On vérifie que ces quatre vecteurs forment un système libre (on peut aussi bien sûr résoudre directement les équations pour le noyau) : par exemple, si en regardant l'avant-dernière ligne, on trouve que . En regardant la troisième ligne, on en déduit que , puis que , , donc que la combinaison linéaire est triviale. Bref, .
Passons à . Les colonnes 1 et 3 de sont égales, les colonnes 4 et 5 sont liées. La dernière colonne est nulle. La somme de la deuxième colonne et de la troisième est liée à la quatrième ! L'image est engendrée par , et on a .
De ces informations, on déduit qu'il y a deux blocs de Jordan de dimension 3 chacun. On a donc
-
Calculer une matrice inversible
(ou
) telle que
.
SolutionOn cherche une base dans laquelle la matrice de est . Pour cela, on choisit un vecteur tel que , par exemple, en notant la base canonique, . On cherche alors une forme linéaire telle que , et . Par exemple, . L'orthogonal du sous-espace du dual engendré par , et est un supplémentaire de stable par . Calculons-le. On a , , L'orthogonal de est donc donné par les équations , , , dont une base est , . On vérifie que est tel que . Donc la matrice s'écrit dans la base , autrement dit si , on a .
Exercice
- Calculer le polynôme minimal de .
- Ecrire la décomposition de Frobenius de
:
en précisant
la valeur de
et la valeur des polynômes minimaux de la restriction de
à
.
- Calculer la dimension des noyaux de pour entier.
Solution
Exercice
Partitions et décomposition de Jordan
Jordan et invariants de similitude
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-8 Exercice : décomposition de Jordan-Chevalley
Soit une matrice de polynôme caractéristique et soit la partie « sans facteur carré » du polynôme , c'est-à-dire le quotient de et de son pgcd par le polynôme dérivé de .
- Soit
un polynôme vérifiant
et
.
Montrer que le polynôme minimal
de
divise
et que
est nilpotente et commute avec
.
SolutionLes congruences se traduisent par et avec deux polynômes et . Comme est le polynôme caractéristique de , on a , donc , ce qui signifie que le polynôme minimal de divise et que est semi-simple (diagonalisable sur ) puisque n'a que des facteurs simples. D'autre part, . Il existe une puissance de qui est divisible par . Donc et est nilpotente.
La décomposition est la décomposition de Dunford (Jordan-Chevalley) de la matrice . - Montrer qu'il existe un polynôme tel que .
- Soit un polynôme. Montrer que .
- On considère la suite de polynômes définis par
,
est le reste de la division euclidienne par
de
(si
,
sont deux
polynômes,
est le composé de polynômes
).
Montrer que
, puis que
.
En déduire que pour assez grand, vérifie et (donner une estimation d'un tel ).
SolutionOn a en utilisant la formule de Taylor queOn en déduit par récurrence queEn prenant supérieur à un entier tel que soit divisible par , on en déduit que . On vérifie alors par récurrence que . doit convenir.
- On prend
et
une matrice de polynôme caractéristique
égal au polynôme
. Que vaut
?
Combien de termes de la suite doit-on calculer a priori pour trouver les matrices
et
de la décomposition de Dunford de A ? Il n'est pas demandé de faire le calcul, mais
de dire quelles opérations seront faites.
SolutionOn a . Comme est un multiple de , . Donc il suffit de calculer . , .
Exercice
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-9 Endomorphisme cyclique et commutant
Proposition
Démonstration
Supposons que est cyclique. Il existe donc tel que . Soit un endomorphisme commutant avec . Le vecteur s'écrit avec puisque est -cyclique. Si , on a et
Supposons que les endomorphismes commutant avec sont de la forme .
Supposons que n'est pas -cyclique. On a alors une décomposition avec stable par avec . La projection de sur parallèlement à commute avec . En effet, si et , alors et et
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VII-10 Carré d'un endomorphisme
Exercice
Exercice
Soit un espace vectoriel de dimension finie et un endomorphisme de nilpotent et cyclique. Montrer que avec et deux sous-espaces vectoriels cycliques pour de dimension respective (entier inférieur le plus proche de ) et (entier supérieur le plus proche de ).
Solution
Soit une matrice d'invariants de similitude .
- Donner les invariants de similitude de
.
SolutionLa matrice est nilpotente. Les dimensions successives des noyaux de sont 4, , , , . Les dimensions successives des noyaux de sont 6, 9, 10. La suite des est 6, 3, 1. Les invariants de similitude de sont (question précédente appliquée à chacun des sous-espaces cycliques pour ou directement (3 = nombre de blocs de Jordan ; 2 = nombre de blocs de Jordan de taille , 2 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille , 1 = nombre de blocs de Jordan de taille .
On peut le voir plus facilement à l'aide des tableaux de Young :
:
:
-
Existe-t-il une matrice
non semblable à
dont le carré est
semblable à
? Si oui, en donner les invariants de similitude.
SolutionLa matrice d'invariants de similitude convient.
On peut vérifier que ce sont les seuls invariants de similitude possible (cela se voit facilement en utilisant les diagrammes de Young).
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
VIII Tous les exercices WIMS utilisés
- Endomorphismes et projecteurs
- Polynômes d'endomorphismes et projecteurs
- Sous-espaces cycliques et invariants
- Nombre de classes de similitude I
- Nombre de classes de similitude II
- Nombre de classes de similitude III
- Diagonalisable ?
- Trouver un vecteur propre
- Matrice diagonalisable ?
- Trouver un vecteur propre
- Matrice diagonalisable ? Peut-on conclure
- Petit QCM sur la diagonalisation
- Matrices nilpotentes et tableaux de Young
- Partitions et décomposition de Jordan
- Pratique de Jordan
- Matrice de Jordan et noyaux itérés
- Partitions et décomposition de Jordan
- Jordan et invariants de similitude
- Pratique de la décomposition de Jordan-Chevalley
- Carré d'un endomorphisme nilpotent
- I Polynômes d'endomorphismes
- II Sous-espaces stables
- III Sous-espaces cycliques
- IV Dualité
- V Facteurs invariants et décomposition rationnelle (Frobenius)
- VI Diagonalisation et trigonalisation
-
VII Décomposition de Jordan
- VII-1 Réduction de Jordan
- VII-2 Formes de Jordan possibles
- VII-3 Dimension de la somme des espaces propres
- VII-4 Exercice : décomposition de Dunford explicitement
- VII-5 Exercice : comment calculer la matrice de Jordan d'un endomorphisme nilpotent
- VII-6 Vecteurs propres
- VII-7 Quelques exercices
- VII-8 Exercice : décomposition de Jordan-Chevalley
- VII-9 Endomorphisme cyclique et commutant
- VII-10 Carré d'un endomorphisme
- VIII Tous les exercices WIMS utilisés