Doc Polyèdres convexes semi-réguliers
Sommaire
Ce document rédigé pour les étudiants de la licence scientifique générale (L3 pour des futurs professeurs des écoles à l'université Paris-Sud) accompagne une partie du cours de géométrie basé sur l'ouvrage de Daniel Perrin : Mathématiques d'école : nombres, mesures et géométrie publié par Editions Cassini (402 p. ISBN 978-2-84225-158-1) . On y fait référence par ME.
ME exercice 187, 185 renvoie à l'exercice 187 de la nouvelle édition, 185 de la première. De même pour les pages ou les propositions.
ME VI.1. renvoie à la partie 1 du chapitre 6.
Le but de ce document est de décrire les polyèdres convexes semi-réguliers. Dans le problème I de [ME.IX] (page 292, 283 ; corrigé page 388, 374), on montre que les polyèdres décrits ici sont les seuls satisfaisant à la définition.
- Polyèdres convexes
- Les polyèdres réguliers ou solides de Platon.
- Les polyèdres semi-réguliers
- Exercices de synthèse
- Les polyèdres dans la nature
- Index des polyèdres
- Références
Pour voir un polyèdre, cliquez sur son nom et soyez patient. Les figures mobiles utilisées pour illustrer ce document sont issues de l' outil polyèdres créé par Bernadette Perrin-Riou sans lien de parenté avec le précédent .
Définitions et premières propriétés.
Nous rappellons ici les définitions et les résultats présentés dans [ME.IX.1 et 2].Définition : Polyèdre convexe
- On appelle polyèdre convexe un solide (plein) P
vérifiant les propriétés suivantes :
- P est l'intersection d'un nombre fini de demi-espaces fermés limités par des plans , ..., (on prendra un système minimal)
- P est borné
- P n'est pas contenu dans un plan
- Les faces d'un polyèdre convexe sont les intersections de P avec les plans frontières . Leur réunion est la frontière de P. Les faces sont des polygones plans convexes dont les côtés sont les arêtes du polyèdre et dont les sommets sont les sommets du polyèdre.
Exercice : Explicitez cette définition pour un cube, une pyramide.
Propriétés
- Le nombre de côtés d'une face est au moins 3.
- Le nombre d'arêtes aboutissant en un sommet est égal au nombre de faces aboutissant en ce même sommet et ce nombre est au moins 3.
- Une arête est commune à deux faces exactement et joint deux sommets.
- Règle de la somme des angles
- Formule d'Euler
Règle de la somme des angles
Patron d'un sommet
On appellera patron du sommet A du polyèdre P une figure plane de toutes les faces aboutissant en A obtenue après découpage selon une arête aboutissant en A et mise à plat.
Voici le patron d'un sommet de cube : 
Aidez vous d'un tel patron pour visualiser la règle de la somme des angles.
Règle de la somme des angles
Une démonstration de cette règle assez évidente visuellement est proposée dans l'annexe du chapitre IX [ME page 298, 280].
Formule d'Euler
Une démonstration de cette formule basée sur la formule de Girard est donnée en [ME.IX.2]
Pour une pyramide à base pentagonale, on a : , et .
Définition et possibilités
Nous rappellons ici les définitions et les résultats présentés dans [ME.IX.3].Définition : Polyèdre convexe régulier
On dit qu'un polyèdre P convexe est régulier si les faces de P sont des polygones réguliers ayant tous le même nombre p de côtés et si en chaque sommet de P aboutissent le même nombre q de faces (ou d'arêtes).
Notation : Un polyèdre régulier est caractérisé par la liste de ses faces (notées par leurs nombres de côtés) en un sommet. On appellera symbole du polyèdre cette liste (voir la définition générale du symbole ). Par exemple, le polyèdre dont toutes les faces sont des triangles qui se groupent par 4 en chaque sommet se note (3,3,3,3) .
Histoire : Les polyèdres convexes réguliers sont aussi appelés solides de Platon (voir [ME.IX. Introduction])
Les possibilités
Voici les patrons possibles pour un sommet entouré de triangles :
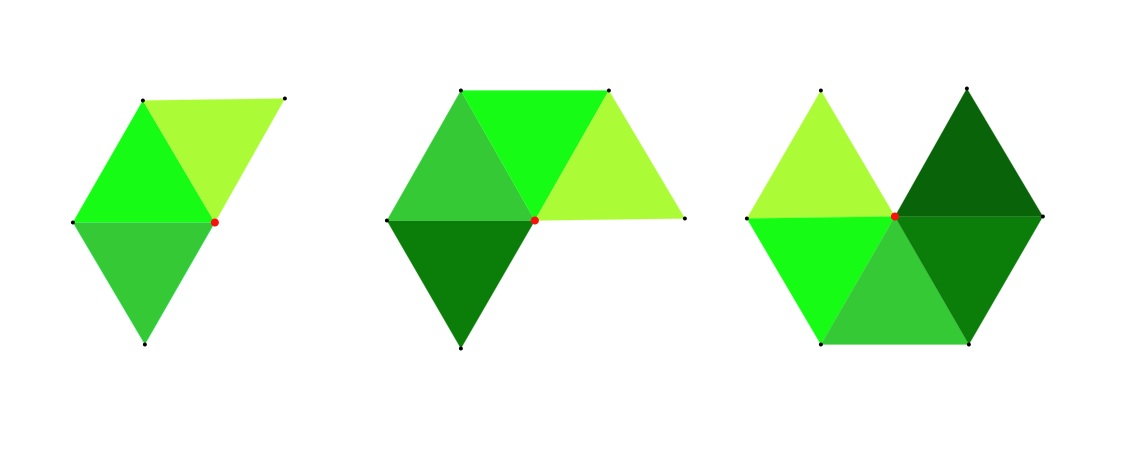
Voici les patrons possibles pour un sommet entouré de carrés, de pentagones :
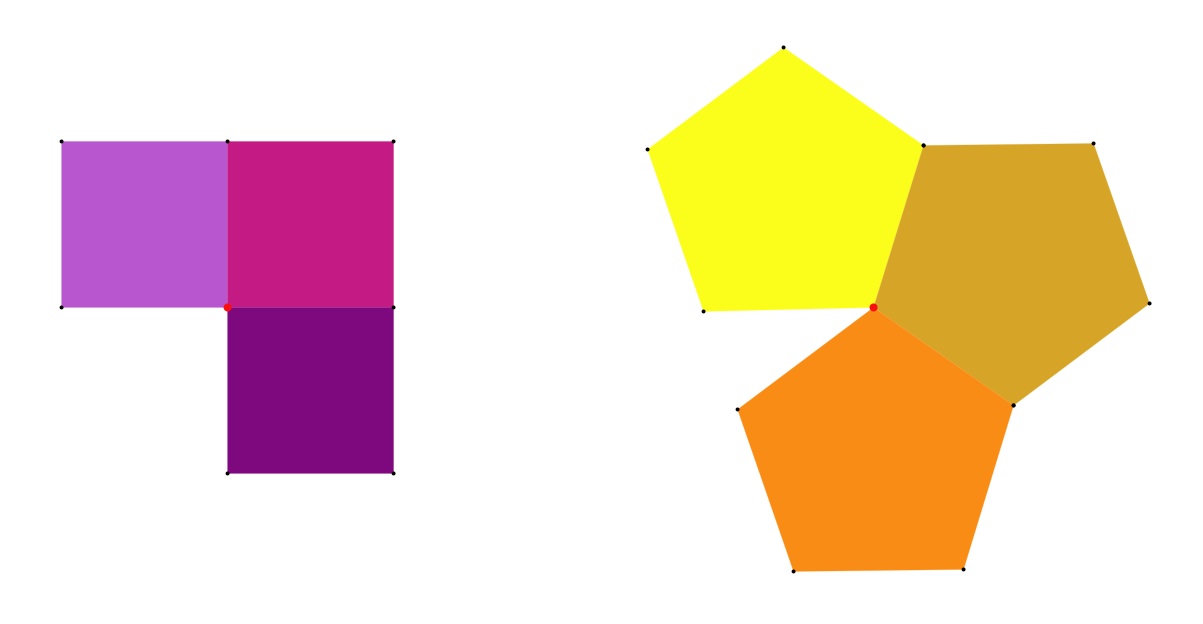
La somme des angles de trois hexagones, heptagones ... dépasse 360°. Donc les polyèdres réguliers ont des faces triangulaires, carrées ou pentagonales.
En résumé, il n'y a que cinq possibilités que nous étudions à la page suivante.
Les polyèdres réguliers
Autour d'un sommet d'un polyèdre régulier, on peut mettre 3, 4 ou 5 triangles, 3 carrés ou 3 pentagones. Il y a donc 5 symboles possibles pour un polyèdre régulier.En utilisant la formule d'Euler , on détermine à partir du symbole d'un polyèdre régulier (ou liste des faces en un sommet) le nombre de ses sommets, de ses arêtes, de ses faces (voir démonstration de [ME.IX.3.3]). Ensuite, il reste à le construire. Le symbole détermine complètement le polyèdre régulier et son nom dépend du nombre de ses faces :
Le polyèdre (3,3,3) est un tétraèdre et possède 4 faces (Le voir et le faire tourner) .
Le polyèdre (3,3,3,3) est un octaèdre et possède 8 faces (Le voir et le faire tourner) .
Le polyèdre (3,3,3,3,3) est un icosaèdre et possède 20 faces (Le voir et le faire tourner) .
Le polyèdre (4,4,4) est un cube ou hexaèdre et possède 6 faces (Le voir et le faire tourner) .
Le polyèdre (5,5,5) est un dodécaèdre et possède 12 faces (Le voir et le faire tourner) .
Exercices :
- Apprenez à les reconnaître !
- Apprenez à écrire leur nom !
Dualité, nombres de sommets et d'arêtes
Si est un polyèdre régulier, imaginons le polyèdre dont les sommets sont les centres des faces de : Le polyèdre est régulier, on l'appelle dual de . Par exemple si est un cube, est un octaèdre. Le dual de est un homothétique de . Donc le dual d'un octaèdre est un cube. Le nombre de sommets de est le nombre de faces de et réciproquement.
Connaître le dual d'un polyèdre régulier permet de retenir son nombre de sommets, le nombre de faces étant indiqué par le nom d'un polyèdre régulier, il suffit de connaître la formule d'Euler pour calculer le nombre d'arêtes. Evidemment, un polyèdre et son dual ont même nombre d'arêtes ( Les nombres de sommets et de faces étant échangés, la formule d'Euler donne le même nombre d'arêtes. ).
| polyèdre | dual |
|---|---|
| tétraèdre (3,3,3) s=4 a=6 f=4 Voir son dual |
|
| cube (4,4,4) s=8 a=12 f=6 Voir son dual |
octaèdre (3,3,3,3) s=6 a=12 f=8 Voir son dual |
| dodécaèdre (5,5,5) s=20 a=30 f=12 Voir son dual |
icosaèdre (3,3,3,3,3) s=12 a=30 f=20 Voir son dual |
Mémorisez les caractéristiques des polyèdres de Platon !
Les polyèdres semi-réguliers
Un polyèdre régulier est semi-régulier.
Toutes les arêtes ont même longueur et les faces de même type sont isométriques.
Remarque. Pour se débarrasser de la paire de faux jumeaux qui ont même symbole , il faudrait affiner la définition. Mais, pour nos objectifs, cet énoncé suffit.Symbole d'un polyèdre semi-régulier
On gardera ces notations tout au long de ce document : est le nombre de faces aboutissant en un sommet et est le nombre de côtés de la plus petite face. La règle de la somme des angles permet d'affirmer que et sont inférieurs ou égaux à 5.
L'ordre lexicographique est l'ordre utilisé pour ranger les mots dans un dictionnaire. On trie les mots par la première lettre, puis on range ceux qui ont la même première lettre par ordre de la seconde lettre ... Le grand rhombicuboctaèdre admet pour symboles rangés dans l'ordre lexicographique : , , , , , .
Le symbole détermine complètement la combinatoire d'un polyèdre, c'est-à-dire les nombres de ses sommets, arêtes et faces de chaque type (voir ici pour un exemple).
On ne cherche pas à démontrer que le symbole détermine un polyèdre semi-régulier à similitude près.
Si on ajoute à la définition d'un polyèdre semi-régulier une condition du type "tous les sommets sont pareils", le symbole détermine le polyèdre semi-régulier à similitude près, sinon on trouve deux polyèdres différents de symbole (cherchez les différences).
Exemple. Le symbole d'un prisme droit régulier pentagonal est . Celui d'un cuboctaèdre est (3,4,3,4).
Exercice. Symbole d'un polyèdre
Règle de parité
La règle de parité
Démonstration : Indiquer le nombre de côtés des faces autour des sommets d'une face à nombre impair de côtés (voir [ME page 389, 375]).
Les symboles possibles
Dans le problème "Les polyèdres archimédiens" ([ME page 292, 283]), on recherche les symboles possibles pour des polyèdres semi-réguliers en s'appuyant sur la règle de la somme des angles , la règle de parité et d'autres raisonnements du même type et on montre qu'il en existe au plus 13 en plus des 5 polyèdres réguliers , des prismes et antiprismes . Pour montrer qu'à chacun de ces 13 symboles correspond un polyèdre semi-régulier, il suffit de construire celui-ci. Dans la suite, on verra comment la plupart s'obtient simplement à partir des polyèdres réguliers et on dressera la liste de tous les polyèdres semi-réguliers.
Exercice 1. Utiliser la règle de la somme des angles et la règle de parité pour faire la liste des seuls symboles possibles vérifiant : et . Même exercice avec , puis . On verra dans la suite de ce document qu'il existe pour chacun de ces symboles un polyèdre semi-régulier.
Exercice 2. Par un raisonnement analogue à la démonstration de la règle de parité, montrer que, dans les symboles de la forme avec , les entiers et sont nécessairement égaux et déterminer tous les symboles de ce type.
Prismes et antiprismes
La référence de cette page est [ME.IX. page 294, 285]
Un antiprisme de base un polygone régulier à côtés ( ) est un polyèdre semi-régulier de symbole .
|
Un prisme régulier a
sommets,
arêtes
et pour faces :
carrés et 2 polygones à
côtés. Voici un prisme à base hexagonale : |
Un antiprisme a
sommets,
arêtes et pour faces :
triangles et 2 polygones à
côtés. Voici un antiprisme à base hexagonale : |
|
|
|
Tronquer un polyèdre
Pour obtenir un nouveau polyèdre à partir d'un polyèdre donné, on peut considérer un polyèdre dont les sommets sont sur les arêtes du polyèdre , c'est-à-dire à tronquer .Le sommet est donc remplacé par la face .
Remarques :
- Des conditions sont imposées au polyèdre à tronquer pour obtenir un polyèdre semi-régulier.
- Dans le document DOC Polygones convexes réguliers , on explique comment tronquer un polygone régulier pour obtenir un nouveau polygone régulier. C'est la première opération à faire en chaque face pour que le polyèdre tronqué ait encore des faces régulières.
Exemple : Tronquer un cube
Tronquer un cube
Vous pouvez faire bouger le point P entre M et B. Les faces roses sont les bases des pyramides retirées. Les octogones verts sont les faces qui remplacent les faces du cube. Si P est en M, on obtient un cuboctaèdre . Si P est en Q, on obtient un cube tronqué .
Les polyèdres archimédiens
Nous allons maintenant énumérer les polyèdres archimédiens . Nous ne justifions pas toutes nos affirmations mais nous nous attachons à décrire les polyèdres pour aider l'imagination. Nous avons choisi de les classer en trois familles qui correspondent à la valeur de , le nombre d'arêtes aboutissant en un sommet, mais aussi à la façon de les obtenir par troncature à partir des polyèdres réguliers.- Rectification : un sommet au milieu de chaque arête.
- Troncature : Deux sommets par arête.
- Les adoucis (q=5)
Les premiers exercices de chaque partie permettent de visualiser les polyèdres ainsi construits en les repérant par leurs symboles.
Un sommet au milieu de chaque arête
Méthode de rectification
On considère un polyèdre semi-régulier tel que de part et d'autre de chaque arête, on ait une face à côtés et une face à côtés.On verra que les seuls polyèdres semi-réguliers qui vérifient cette hypothèses sont les polyèdres réguliers, le cuboctaèdre et l'icosidodécaèdre.
On considère le polyèdre dont les sommets sont les milieux des arêtes de , c'est-à-dire qu'on coupe le polyèdre en chaque sommet selon un plan passant au milieu des arêtes. On dit que est le rectifié de .
Soit une arête de et son milieu. Les faces de aboutissant en M sont au nombre de 4 :
- une face polygone régulier à côtés tracée sur la face à côtés de (mais plus petite),
- une face correspondant au sommet donc à côtés (si on est assuré que les milieux des arêtes de sont dans un même plan),
- une face polygone régulier à côtés tracée sur la face à côtés de (mais plus petite),
- une face correspondant au sommet donc à côtés.
Voici la méthode appliquée au patron du sommet d'un octaèdre :
Les faces triangulaires bleues sont portées par les faces de l'octaèdre. Les faces carrées orange sont les bases des pyramides ôtées.
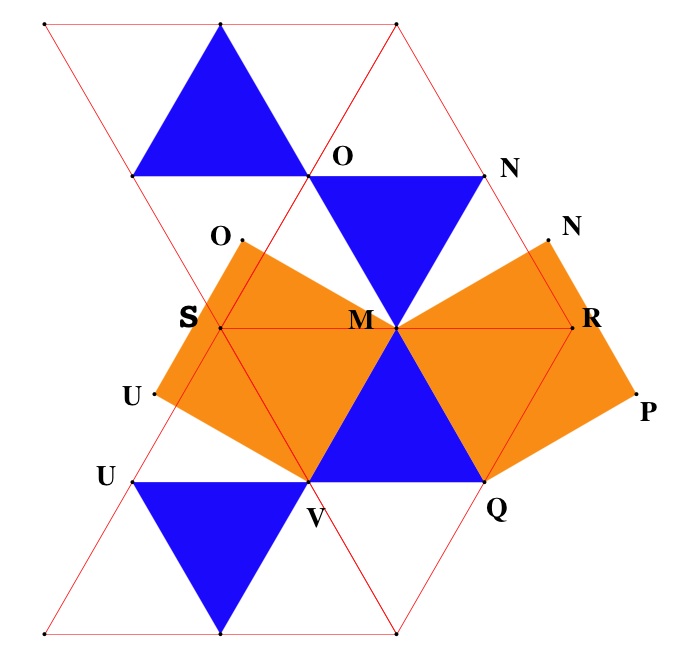
Combinatoire du polyèdre rectifié.
Le polyèdre , rectifié de , a sommets (un par arête de ), autant de faces à ou côtés que , faces à côtés et arêtes puisque par la formule d'Euler , on a .
Quel résultat ?
Dans le cas où est régulier, et sont égaux, notons leur valeur commune. Alors les faces à côtés de correspondant aux sommets de sont des polygones réguliers. Le polyèdre est semi-régulier et son symbole est à permutation circulaire près.
Dans le cas où est semi-régulier sans être régulier, Le polyèdre n'est pas semi-régulier, en effet ses faces à côtés, bases des pyramides ôtées, ne sont pas régulières. Pourtant il existe un polyèdre semi-régulier de même combinatoire (même symbole, mêmes nombres , et ), appelé petit rhombi...
Cuboctaèdre et compagnie
Les polyèdres obtenus par la rectification vérifient . Et ce sont les seuls avec les antiprismes et l'octaèdre obtenu par rectification du tétraèdre. La rectification de deux polyèdres réguliers duaux donne le même polyèdre semi-régulier.
| Polyèdres réguliers |
Polyèdres semi-réguliers un sommet au milieu de chaque arête |
|---|---|
|
(3,3,3) Tétraèdre régulier 4s 6a 4 triangles |
(3,3,3,3) Octaèdre |
| (4,4,4) Cube 8s 12 a 6 carrés |
(3,4,3,4)
Cuboctaèdre
12s 24a 6 carrés et 8 triangles |
| (3,3,3,3) Octaèdre 6s 12a 8 triangles |
|
| (5,5,5) Dodécaèdre 20s 30a 12 pentagones |
(3,5,3,5)
Icosidodécaèdre
30s 60a 12 pentagones et 20 triangles |
| (3,3,3,3,3) Icosaèdre 12s 30a 20 triangles |
Les petits Rhombi...
On peut rectifier un cuboctaèdre ou un isosidodécaèdre. Les polyèdres obtenus ne sont pas semi-réguliers mais le petit rhombicuboctaèdre et le petit rhombicosidodécaèdre sont les polyèdres semi-réguliers de même combinatoire :
Le petit rhombicosidodécaèdre a pour symbole (3,4,5,4). Il a 60 sommets, 120 arêtes et pour faces 20 triangles, 30 carrés et 12 pentagones.
Exercice. Sommets au milieu des arêtes
Deux sommets par arête
Tronquer un polyèdre régulier
Soit un polyèdre régulier
admettant s sommets, a arêtes et f faces à n côtés.
Considérons deux points sur chaque arête de
posés de sorte que sur chaque face de
le polygone de sommets les nouveaux points soit régulier (
comment ?
).
Il a donc 2n côtés. Le polyèdre
dont les sommets sont les nouveaux points est appelé
polyèdre tronqué de
,
il est semi-régulier par construction. Il a
sommets et
faces à
côtés.
Exemple.
Voyons, sur l'exemple de l'octaèdre, quelle est l'allure d'un sommet du polyèdre . Nous avons tracé le patron d'un sommet S de et, sur les arêtes aboutissant en , posé les sommets de . Par exemple et se trouvent sur l'arête . Les faces hexagonales de sont bleues. Autour du sommet , on a donc deux faces hexagonales et une face à côtés obtenue en tronquant le sommet , ici, c'est un carré.
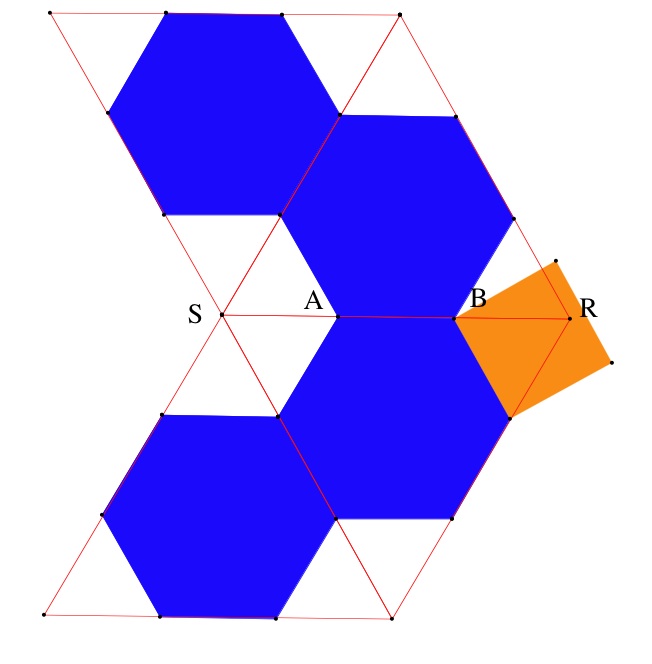
En chaque sommet de
aboutissent
arêtes, pour obtenir
, on enlève une petite pyramide (on tronque le sommet de
) et
on le remplace par une face à q côtés qui est la base de la pyramide enlevée,
a donc s faces à q côtés.
Le
symbole
de
est
. Comme
vaut au moins
et
au plus
, l'ordre du symbole est bien respecté, la
règle de parité
aussi.
Exemple : Aperçu de l'
octaèdre tronqué
. Son symbole est (4,6,6).
Par la formule d'Euler on obtient le nombre d'arête de qui égale .
Tronquer un polyèdre semi-régulier, non régulier
Si on veut appliquer cette méthode de troncature à un polyèdre semi-régulier, on doit imposer à celui-ci que de part et d'autre d'une arête se trouvent une face à côtés et une face à côtés (Les seuls polyèdres semi-réguliers qui vérifient cette hypothèses sont le cuboctaèdre et l'icosidodécaèdre.
) mais on est embarrassé pour placer les deux sommets sur une arête ( pourquoi ? ). Dans tous les cas, le polyèdre obtenu ne sera pas semi-régulier bien que tous ses sommets aient même aspect. Par exemple, à partir d'un cuboctaèdre, on obtient un polyèdre de symbole . Les polyèdres semi-réguliers qui ont la combinatoire de ces polyèdres tronqués sont les grands rhombi...Comment tronquer un polyèdre ?
Quand on tronque un polyèdre régulier, on enlève une petite pyramide en chaque sommet du polyèdre en coupant par un plan à une distance (sur l'arête) de chaque sommet. Chaque face à côtés du polyèdre régulier porte alors une face à côtés du polyèdre tronqué. Cette face est encore un polygone régulier si on a tronqué le sommet à la distance où est la longueur de l'arête. (Voir DOC Polygones convexes réguliers )Quand le polyèdre à tronquer est semi-régulier sans être régulier, par exemple, si en chaque sommet, aboutissent des carrés et des triangles, on ne sait plus à quelle distance tronquer pour que les nouvelles faces soient régulières. En effet, si on tronque à un tiers du sommet, les octogones obtenus sur les faces carrées ne seront pas réguliers ; si on tronque à une distance du sommet (avec longueur des arêtes), les hexagones obtenus sur les faces triangulaires ne seront pas réguliers.
Polyèdres tronqués (vrais ou faux)
Les polyèdres tronqués
Tous les polyèdres archimédiens obtenus par troncature vérifient et ce sont les seuls polyèdres semi-réguliers vérifiant avec les prismes , le tétraèdre, le cube et le dodécaèdre et les faux tronqués (voir plus bas). Chaque nom de polyèdre est un lien vers son animation.
| Polyèdres réguliers | Polyèdres semi-réguliers deux sommets par arêtes |
|---|---|
| (3,3,3) Tétraèdre régulier 4s 6a 4 triangles |
(3,6,6)
Tétraèdre tronqué
12s 18a 4 triangles et 4 hexagones |
| (4,4,4) Cube 8s 12 a 6 carrés |
(3,8,8)
Cube tronqué
24s 36a 8 triangles et 6 octogones |
| (3,3,3,3) Octaèdre 6s 12a 8 triangles |
(4,6,6)
Octaèdre tronqué
24s 36a 6 carrés et 8 hexagones |
|
(5,5,5) Dodécaèdre 20s 30a 12 pentagones |
(3,10,10)
Dodécaèdre tronqué
60s 90a 20 triangles et 12 décagones |
| (3,3,3,3,3) Icosaèdre 12s 30a 20 triangles |
(5,6,6)
Icosaèdre tronqué
(ballon de football) 60s 90a 12 pentagones et 20 hexagones |
On peut trouver des icosaèdres tronqués "naturels" sur cette page : Des icosaèdres tronqués .
Les grands rhombi... ou faux tronqués
Voici deux polyèdres semi-réguliers dont les symboles pourraient résulter d'une telle opération de troncature (sur quels polyèdres ?). Ce sont les grands rhombi... (ou faux tronqués). Ils ont la combinatoire des polyèdres tronqués.Le grand rhombicosidodécaèdre a pour symbole (4,6,10). Il a 120 sommets, 180 arêtes et pour faces 30 carrés, 20 hexagones et 12 décagones.
Exercices.
- Reconnaître sur une figure un polyèdre obtenu par troncature
- Reconnaître un polyèdre (obtenu par troncature) donné par son symbole
- Décrire un polyèdre obtenu par troncature
Les adoucis
Comment classer ou caractériser ces deux derniers polyèdres archimédiens ? Avec l'icosaèdre, ce sont les seuls qui vérifient : en chaque sommet aboutissent 5 faces. Ensuite grâce à la règle de la somme des angles, les cas possibles sont vite énumérés.Le cube adouci a pour symbole (3,3,3,3,4). Il a 24 sommets, 60 arêtes et pour faces 32 triangles et 6 carrés.
Le dodécaèdre adouci a pour symbole (3,3,3,3,5). Il a 60 sommets, 150 arêtes et pour faces 80 triangles et 12 pentagones.
Pour comprendre le nom d'adouci, il faut imaginer qu'on a pris un cube par exemple et qu'on a adouci ses sommets et ses arêtes par des triangles et obtenu ainsi un cube adouci. Plus précisément, on a 6 faces carrées qui correspondent à celles du cube, 8 faces triangulaires à la place des sommets et 2 faces triangulaires par arête du cube soit en tout 32 triangles. Chaque sommet du cube adouci appartient à une face carrée et une seule (voir le symbole) donc le cube adouci a sommets. Le nombre d'arêtes calculé par la formule d'Euler est .
Exercice : Calculer du dodécaèdre adouci en utilisant les relations entre s, a et f. ( Solution )
Exercices de synthèse
- Généralités sur le symbole
- Classer les polyèdres selon le nombre d'arêtes en un sommet
- Nommer un polyèdre donné par son symbole
- Décire un polyèdre semi-régulier donné par une figure (1)
- Reconaître les rhombi ...
- Nommer les rhombi...
- Décrire un polyèdre semi-régulier donné par une figure (2)
Les polyèdres dans la nature
Molécules chimiques
La molécule de méthane a la structure d'un tétraèdre régulier. Voir aussi Géométrie moléculaire tétraèdrique.
La molécule de hexafluorure de soufre a la structure d'un octaèdre régulier. sur Wikipédia
Dans l'art
Paul Sérusier peint ce tableau en 1910. Il est au musée d'Orsay.

Un isocaèdre sur une place d'Amsterdam.
Des icosaèdres tronqués
L'icosaèdre tronqué est répertorié sur cette page . Comme sur cette page , on peut décrire sa structure : Un icosaèdre régulier admet 12 sommets, 30 arêtes et 20 faces triangulaires. On tronque cet icosaèdre au tiers des arêtes : on obtient à la place de chaque sommet une face pentagonale et chaque face triangulaire de l'icosaèdre est réduite en une face hexagonale de l'icosaèdre tronqué. Chaque sommet de l'icosaèdre tronqué provient d'un point au tiers d'une arête de l'icosaèdre, il y a donc 60 sommets où arrivent un pentagone et deux hexagones. Le symbole de ce polyèdre semi-régulier est (5,6,6).
L'icosaèdre tronqué le plus roulant est le ballon de football.
L'icosaèdre tronqué décrit une molécule composée de carbone, le fullerène , voyez cette page Wikipédia.
Voici des vues d'une maison à Torshavn (Iles Féroé) qui présente en partie la même forme.
Index des polyèdres
Le lien renvoie à la page de ce document où le polyèdre est décrit. Vous pouvez utiliser l' outil polyèdres pour les visualiser.- Tétraèdre
- Octaèdre
- Icosaèdre
- Cube
- Dodécaèdre
- Prisme régulier
- Antiprisme
- Cuboctaèdre
- Icosidodécaèdre
- Petit rhombicuboctaèdre
- Petit rhombicosidodécaèdre
- Tétraèdre tronqué
- Octaèdre tronqué
- Icosaèdre tronqué
- Cube tronqué
- Dodécaèdre tronqué
- Grand rhombicuboctaèdre
- Grand rhombicosidodécaèdre
- Cube adouci
- Dodécaèdre adouci
Références
Livres et papiers
- La référence principale pour les définitions et les résultats fondamentaux est Mathématiques d'école . Les démonstrations proposées dans cet ouvrage (et omises dans ce résumé) sont accessibles aux lycéens.
- Un ouvrage de pliage pour fabriquer des polyèdres : Pliages et Mathématiques de Didier Boursin et Valérie Larose aux Editions du Kangourou
- en particulier le pliage d'un tétraèdre.
- Sur le site du Kangourou des mathématiques, vous trouvez des fascicules sur le sujet et des patrons de tous les polyèdres.
- Patrons à télécharger
Sites
- Wikipédia : Solides d'Archimède
- Les polyèdres en mouvement 2 : Vous pouvez les faire tourner avec la souris
- Pour aller plus loin